A trading function is used to define and keep a constant function market maker stable. It keeps track of the assets supplied to the CFMM by liquidity providers and updates it continually as trades occur; it is also responsible for defining the CFMMs invariant which is an expression that must be kept constant for all trades.
The trading function of a CFMM is its most important aspect as it defines almost all its other properties, including the payoff agents can expect when they interact with it. In this article, we'll study the major components of a trading function which go on to define the behaviour of a CFMM.
This work is mostly an aggregation and distillation of multiple research papers and the continuation of previous work. It is academic shitposting by a nonacademic hobbyist and might not interest most as it proposes no novel results, it merely intends to propagate said results in a more informal setting. There might be mistakes in spelling, or misunderstandings of the tech, those are all my mistakes and is why you should definitely read the referenced research as well! Thank you and happy reading.
The trading function is used to define four major functions which go on to define the CFMM's behaviour, they are;
the invariant
The invariant is defined when the reserves are balanced and no trades are occurring, i.e. the invariant is defined purely from the available reserves at any point. This invariant is to be kept fairly constant during trades and is also used to determine the exchange rate between assets based on their available reserves.
the marginal price
The marginal price is defined as the instantaneous rate of change of assets' prices due to a minute change in their reserve values i.e. due to a negligible trade. It can also be understood as the "price" for the smallest possible trade.
In the previous article, we defined marginal prices as the first order taylor approximation of the trading function. while this definition is correct it is a bit cumbersome. A simpler mathematical definition for this concept is; the absolute value of the partial derivative of the trading function with respect to its first argument, divided by the partial derivative with respect to the second argument as the trade sizes tend to zero. The arguments here represent the evolving reserves. Thus a simpler mathematical model for this value is the absolute value of the first differential of the CFMM's invariant.
the curvature
The curvature of a trading function could be trivially described as a measure of how sensitive a market is to variations in its reserves which primarily occur due to trades, and liquidity addition/subtraction. It can be computed as the second derivative of the trading function. It is a global characteristic which essentially measures how convex the trading function is and is intuitively independent of trade sizes and reserve values.
Generally, low curvature CFMMs are less sensitive to reserve variations and are able to offer a stable exchange rate over larger reserve changes. The reverse is also true for high curvature CFMMs, i.e., they are very sensitive to variations in reserve quantities and do not offer stable exchange rates.
the price impact function
The price impact function is used to describe/establish a relationship between a trade's size and its effect on the price of an asset. It represents how the prices of assets change due to finite variations in their reserves due to any arbitrary trade size. It is the cumulative effect of the marginal price over the trade's size, or more simply- the summation of the marginal price(s) over which a trade is settled. Thus it is mathematically computed as the integral of the marginal price over the trade's size.
Now, let us examine these concepts in the context of associated trading functions.
An important guide for the mathematical notations we use here is;
i = r_i × p_i
where i is a placeholder for an asset’s reserve dollar value (or its value relative to any other numeraire)
and ∆_i represents a subset/subdivision of i.
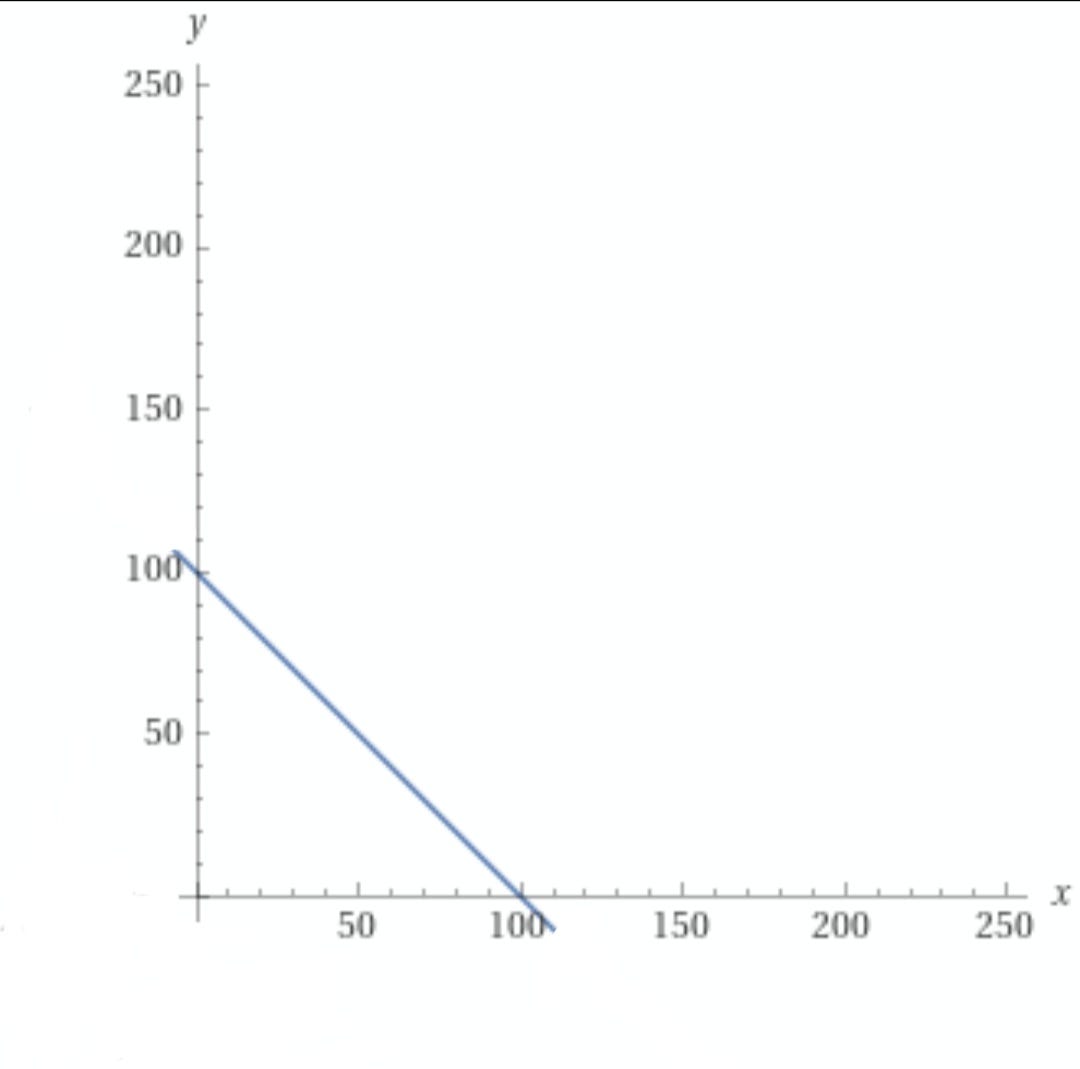
Linear Trading function (Constant Sum Market Makers)
The linear trading function is defined for an n-asset CFMM as
I'll mostly focus on the two-asset case here because it’s the prevalent design, and i also don’t want to deal with multivariate calculus at this point in my life.
invariant/pricing function
ψ(x,y,0,0) = (x - ∆_x) + (y + ∆_y)
when ∆_x = ∆_y = 0
k = (x - 0) + (y + 0)
k = x + y
ie
marginal price
the invariant; k = x + y
since we're using asset X as the numeraire, the differential is defined with respect to it. Thus
y = k - x
y' = 0 - 1
y' = -1
|y'| = 1
thus the marginal price of a linear trading function is ALWAYS equal to unity, as long as the proposed trade can be satisfied with existing reserves.
Remember that this parameter is a measure of variation in exchange rates, thus being equal to one implies that the exchange rate is strictly constant in linear function CFMMs.
The reported price on a CSMM is always equal to the marginal price as the exchange rate between the numeraire and traded asset is expected to be static.
curvature
if it wasn't already obvious from the name, then intuitively from the marginal price, we know that the second derivative of the linear trading function is equal to zero. Thus this trading function is referred to as a "zero-curvature" trading function.
These results highlight that a constant sum market maker, or any other CFMM which utilises a linear trading function maintains a fixed price within a range of trade sizes dependent on its reserves, thus exhibiting price stability with zero curvature.
A constantly static exchange rate is an impossible feat for any financial asset, so this feature doesn't scale. Due to variations in exchange rates on other marketplaces, a constant exchange rate marketplace is basically free money. arbitrage trades will be executed in any number of ways by any number of market participants, till the reserve of any one mispriced asset is empty.
Summarily, this function, while great for trading between assets with equivalent value, isn't scalable as it prices assets at a constant rate in a dynamic environment, leading to reserve deprecation and devaluation due to arbitrage.
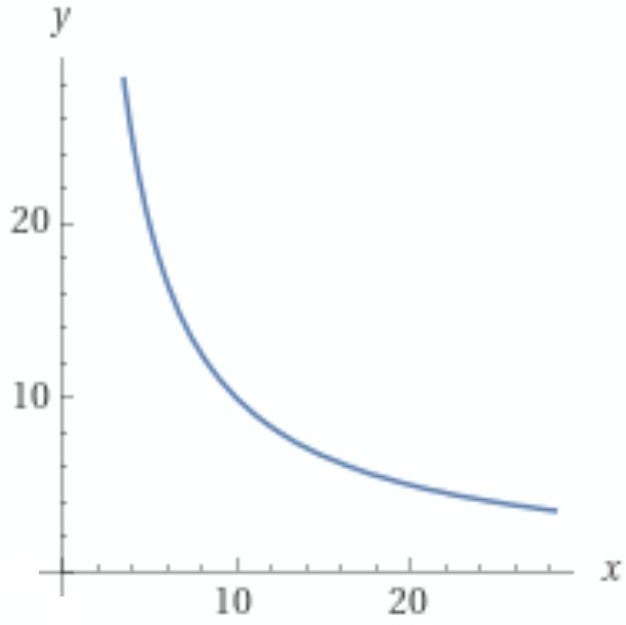
Geometric Trading Function (Geometric Mean Market Makers)
defined as:
geometric market makers are best known for their ability to support up to n number of assets with varying or equal weights, w_n. To avoid confusion and simplify representations, let's limit n to two assets with varying weights.
NB: the sum of the assigned weights of all assets traded using the geometric function is always equal to one.
As earlier, the trading function is defined from the trader's perspective, and asset X is the numeraire which they use to purchase asset Y.
invariant
[the invariant here is commonly expressed as the product of an arbitrary number of assets with specified weights]
To obtain the invariant for this trading function, we assume the reserves are balanced with no trades occurring.
ψ(x,y,0,0) = (x - ∆_x)^{w_x} × (y + ∆_y)^{1 - w_x}
where ∆_x = ∆_y = 0
k = (x - 0)^{w_x} × (y + 0)^{1 - w_x}
ie
marginal prices
k = x^{w_x} × y^{1 - w_x}
simplifying further;
Intuitively, the marginal price for any asset pair in this setting greatly depends on their weights.
curvature
The curvature can only be expressed trivially when the weights are explicitly known.
Hybrid Trading Functions
Only two trading functions are existent so far, with "overkill" features. The linear offers function offers zero curvature but doesn't suit the market it exists in, its geometric counterpart offers convex curvature and ensures nonzero reserves but is prone to high levels of divergence loss and slippage.
So intuitively, the best way to obtain the best features of both designs would be to combine them in some ratio depending on the intended market, but even this combination isn't without costs.
In this section we'll dive into the methods that could theoretically be implemented to combine these trading functions and give an overview of the advantages and disadvantages of each method.
a. Arithmetic mixing:
here the novel trading function is obtained as the weighted arithmetic mean of the linear and geometric trading functions, so that the curvatures of each function may be easily transitioned into each other through a simple arithmetic process. The assigned weight parameter in this case is typically a constant value responsible for causing the trading function to behave more like any of its component functions.
The generalised representation for this construction is
where "t" is the assigned weight and may be any arbitrary value between 0 and 1.
so that as t tends to zero, the function behaves more like a geometric trading function.
This methodology has some advantages including
simplicity due to linearity
least complex mixing mechanism
This method is currently in use in the Curve protocol, which is a low-curvature CFMM optimised for stablecoin exchanges.
b. Geometric mixing:
the linear and geometric trading functions are blended into one function by computing their geometric mean square. The mixing parameter is again, a static value which seeks to emphasise one of the construction's component functions.
The generalised representation for this construction is
again "t" is the assigned weight and the function behaves more like a geometric trading function as t tends to zero.
c. Homotopy mixing:
before we delve into the application of this concept to CFMMs, let us do a bit of an overview.
Homotopy can be very loosely defined as a method used to associate geometric regions by studying the paths within the regions' intersection. It permits two continuous functions to be deformed into each other in a stepwise manner.
In the context of CFMMs, this mechanism may be implemented to dynamically adjust the mixing parameter itself over time i.e., the mixing parameter is designed to be constantly evolving at some rate determined by the homotopy function as trades are occuring. As shown1 by Alexander Port and Neelesh Tiruviluamala, a typical homotopy construction could be able to smoothly morph one trading function into another using two arguments- the trade size and the mixing parameter.
This design also enables the addition of more variables to the trading function in order to ensure the best price possible at any time and under any circumstances. These variables may be
epoch-based,
volume-based,
volatility-based etc.,
depending on the designer's goals and target market.
This design comes with a lot of tradeoffs and is still being researched, so there are no practical iterations yet afaik.
Equivalency of Trading Functions
So we've established that at this point, there are only two distinct trading functions for CFMMs which can be combined through any number of methods to obtain more complex functions for use in more dynamic markets. But does this mean all these functions are only applicable to a specific type of asset/market? Well, yes and no.
Trading Functions may be optimised for a particular type of market but they can still retain the ability to satisfy trades in a different type of market. A practical example of this is the Uniswap trading function which is optimised for volatile markets but can still facilitate stablecoin <> stablecoin trades and even with more volume than Curve whose curvature best suits the purpose.
The ability of a trading function ψ_a to satisfy similar trades with a second trading function ψ_b is referred to as "trading function equivalence".
[The most obvious implication here is that all trading functions are equivalent at a zero trade].
So how exactly can we know CFMM A will be able to satisfy trades just like CFMM B? Well, the common way is simply to "do the trade" and see if it works out; another more complex but more operationally sound method is to use the "trading set" theory propounded initially in the research paper2 by Angeris et al.
Basically, if the trading sets of both CFMMs are equivalent or one is a subset of the other, then they can satisfy the same trades to the extent of their equivalence and are thus equivalent. So what is a trading set and how do you obtain one for a given tracing function at any set of reserves?
A trading set can trivially be described as the set of allowable trades at some fixed reserve value.
The optimal trade is meant to be carried out along the curvature's boundary. However, alternative trades exist within the boundary (important to note that alternative doesn't imply better). Thus an optimal trade along with its alternatives at a fixed reserve value make up the elements of the trading set3.
A simplification of the trading set's core properties include that;
it scales directly with liquidity addition and removal.
two trading sets may be added to obtain a new, larger trading set.
it is convex so that as users trade in more of a token, they will usually receive less, subject to the trading function.
a trader is allowed to ‘overpay’ for a given trade and this new trade would still be considered valid.
a CFMM has a finite amount of assets that it is allowed to tender for a single trade at a given reserve value which is referred to as the "reachable reserve set".
Summarily, if there exists one trade which is feasible in two CFMMs- A and B, with different trading functions- ψ_a and ψ_b respectively; then the trading sets of both CFMMs are equal for that particular trade value and thus their functions are equivalent at that point only.
Another sufficient condition for equivalence between two trading functions is that they should be related by an invertible transformation, f. Basically, if a set of reversible mathematical operations can be carried out on ψ_a to make it equal to ψ_b exists, then both trading functions are equivalent².
In math speak- for any two distinct CFMMs, CFMM A and CFMM B, each with their own trading functions, associated reserves and trading rules; if there exists an invertible transformation function, denoted as f, with an inverse function, f⁻¹ (the inverse) such that f⁻¹(f(x)) = x for all x, which can be applied to the trading function of CFMM A to make it resemble the trading function of CFMM B; then the two trading functions are equivalent and both CFMMs can satisfy the same type of trades allowed under the invertible transformation.
The simplest practical example of this equivalence is seen in constant (geometric) mean market makers, CMMMs, and a special subset, constant product market makers, CPMMS.
Constant Product Market Makers :-
The invariant for CMMMs is expressed as
CPMMs are obtained when we strictly have two assets with equal weights so that
k = (p_x × r_x)^{w_x} × (p_y × r_y)^{w_y}
where w_x = w_y = ½
(since the sum of the weights is strictly equal to one (1), the weight of each asset in a CPMM is equal to ½).
but this value is the CPMM's liquidity, L, which may also be seen as the sum of all the (tradeable) liquidity deposited by liquidity providers. Thus
squaring this equation simplifies to the common invariant for CPMMs;
Thus, the geometric mean of the quantities available in a CPMM is mostly used when it's important to refer to the pool's "money value", while the geometric mean square is used as the invariant to compute trades.
Reversing this stepwise process will lead us right back to the general geometric trading function's invariant. So we've just shown that a Constant Mean Market Maker will be able to satisfy the same trades as a Constant Product Market Maker, provided the weights of the two assets being exchanged are equal.
The trading function of a constant product market maker is expressed as follows;
We can also easily obtain the marginal price by simple arithmetic in our obtained expression for the general case
|y'| = (w_x/1 - w_x) k^{1/1 - w_x} × x^ {-1/(1 - w_x)}
Now we know that the weights are ½, so we can substitute this value and be done. But first we must remember that the obtained expression when we are using the actual weights of the reserves is for their liquidity, L, not their invariant k. So that
from previous results; L² = k, so that
We can also verify this by differentiating the invariant directly
y = k × x^-1
y' = -k × x^-2
With this article, we've mostly covered what it is that allows us to swap our ETH for the dogcoin of the day (or our USDT for USDC) in an abstract setting.
Thank you for your time, hope you enjoyed reading this! Next article will be less tech-y and will be ready soon, do subscribe if you enjoy ramblings on ‘the tech’. Thank you again.
arXiv:2203.12123v3 [q-fin.TR]
arXiv:2003.10001v4 [q-fin.TR]